Basic Paxos

详细梳理Basic Paxos算法，试图找出从Paxos到Raft的演进过程。

引言 (1)

Paxos是公认的最晦涩的协议之一，并且协议和实现之间有着巨大的鸿沟。然而，Paxos却是最重要的一致性协议，甚至成为一致性的代名词。Mike Burrows, inventor of the Chubby service at Google, says that “there is only one consensus protocol, and that’s Paxos”。所以理解Paxos至关重要。Raft只是Paxos的一个简化版本，且性能不及Paxos，但它却因容易理解和实现而迅速流行。我最初接触的是Paxos，理解不很深刻；后来的项目中使用Raft，一下子开朗了很多。机缘巧合，目前项目采用的ceph实现了Paxos，所以我趁此机会再次梳理它：结合ceph-mon中的实现，从Raft的角度，重读论文，理解了大神John Ousterhout和Diego Ongaro根据Paxos提出Raft的思路。这里把心路历程总结一下，方便以后查阅，也希望能和大家交流。理解不到位甚至不正确的地方，还望指正。

复制状态机(Replicated State Machine)是分布式理论中的重要概念：位于不同服务器上的多个状态机(State Machine)在持续运行中维持着一致的状态(State)。容易想象，假如有了Replicated State Machine，分布式系统中遇到的很多问题就迎刃而解，例如一致性、容错等。

如何实现Replicated State Machine呢？复制日志(Replicated Logs)是最常用的方法。以黑盒的方式看，Replicated Logs就是这样一种机制：它能够把client发给状态机的一个个command，以log的方式复制给各个状态机。换言之，无论如何延迟、丢包、重传和重启，最终各个状态机能够得到数量、内容和顺序都严格一致的log序列(command序列)。容易理解，Replicated Logs可以推导出Replicated State Machie，这里用自然语言不严格地描述一下：

• 我们这里讨论的状态机是确定的(Deterministic)，即处于相同状态的状态机，在处理相同的指令(command)之后，下一个状态是确定的；
• 所有状态机初始状态一致，都是空的；
• 所有状态机处理完第一条log之后，状态是一致的，因为log内包含的command是相同的；
• 以此归纳：假如处理完第N条log之后，所有状态机的状态是一致的。由于第N+1条log包含的command相同，所以处理完第N+1条log之后所有状态机的状态是相同的；

下图表示Replicated Logs实现的Replicated State Machine:

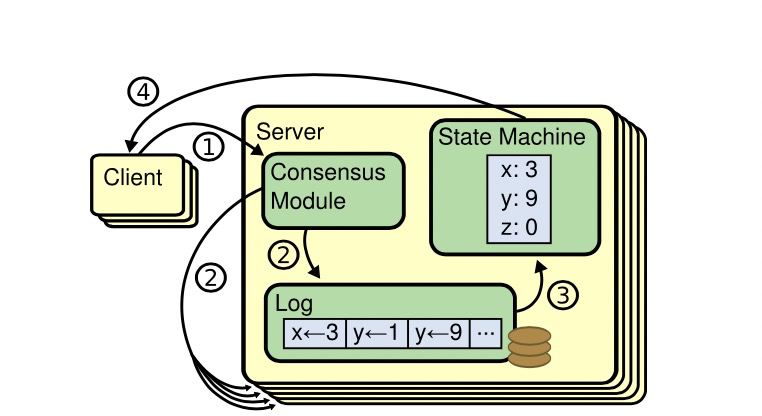
问题 (2)

首先明确，Basic-Paxos的目的是：选定一个值。这与Replicated Logs还相差甚远，但它是形成Replicated Logs的基石：一个Basic-Paxos实例确定一条Log的值，即就一条Log达成一致。一个Basic-Paxos实例内可能发生多轮投票，但最终就是选定一个值。很多人认为每一轮确定一条Log的值，甚至有些文章都这么写，这就谬以千里了。重申一遍，Basic-Paxos不解决Replicated Logs的问题，只是选定一条Log的值。至于如何实现Replicated Logs，我将在Multi-Paxos讲述，现在着眼于如何选定一个值。

这个问题没有看上去那么简单，为了模拟真实分布式场景，问题假设是在一个异步的非拜占庭的模型中：

• 虽然消息不会被篡改，即模型是非拜占庭的；
• 但是每个实体运行速度有快有慢，并且可能随时崩溃、停机、重启；
• 并且每条消息的传播延迟可长可短，并且可能被重传或者丢失；

在这样的环境中有一组进程，它们有一个共同的变量（即各自持有这个变量的一个副本），每个进程都可以为这个变量提议不同的值。现在我们要为变量选定一个值。首先要保证安全需求：

• 只有被提议的值才可能被选定；
• 只有一个值能被选定，我们简称”唯一性”：即最终各个变量副本被赋予相同的值；
• 只有被选定的值，才能被学习到：即只有值被选定了，进程才能学习到它；

这几条都是显而易见的需求，除”唯一性”之外，其它两条如何保证也直观地体现于算法流程中。所以，Basic-Paxos的重点是如何保证”唯一性”。

除了安全需求，还有一个Progress需求，即只要足够多的实体活着，就应该能选定一个值，不能无限空转下去。Basic-Paxos也不解决这个问题，只是这个问题比较容易解决。见第7节。

角色 (3)

针对上述问题，为了方便描述，抽象出以下3中角色。注意，角色是抽象的，第2节中的”进程”同时担任这3中角色。

• Proposer：负责提议Proposal。Proposal包含Proposal Number(简称PN)和Value两部分，一个PN=n且Value=v的Proposal记作Proposal{n, v}。在有些只关心PN而不关心Value的上下文中，也记作Proposal{n}；还有一些上下文，直接记作Proposal，但要清楚其包含PN和Value。
• Acceptor：负责决策，即根据自己所知的信息，回应Proposer发来的请求(下文将看到，有PrepareReq和AcceptReq两种请求)。要强调的是，一个Acceptor如何回应Proposer，完全基于自己记录的信息，不会也无法考虑别的Acceptor。只要每个Acceptor都按算法的的要求如实回应，最终自然能选定一个Value。
• Learner：发现选定的Value。Value虽然是由Acceptor选定的，但是，是Learner发现它被选定这一事实的。

流程 (4)

Prepare阶段 (4.1)

• Prepare(a)：Proposer生成一个PN，设为n，然后向majority个Acceptor发送Prepare请求。Prepare请求只包含PN不包含Value，记作PrepareReq{n}。

• Prepare(b)：一个Acceptor收到PrepareReq{n}时，若n>MaxRespondedPN(即满足下面承诺1)就响应(respond)**它。响应是指持久化MaxRespondedPN=n，并作如下”两个承诺，一个应答”。其中MaxRespondedPN是自己曾经响应过的最大的PN**，它只是一个PN，没有Value。

  • 承诺1：以后只响应(respond)满足PN>n的PrepareReq，不再响应PN<=n的PrepareReq；
  • 承诺2：以后只接受(accept)满足PN>=n的AcceptReq{Proposal}。注意，可以接受PN=n的AcceptReq{Proposal}；显然，这个Proposer马上就会发来PN=n的AcceptReq{Proposal}，正常情况下(没有其他Proposer干扰)要接受，这样才能选定一个值；
  • 应答：给Proposer发应答消息。应答消息记作PrepareResp{Promise{n, MaxAcceptedProposal}}。其中n来自PrepareReq{n}，表示对PN=n的PrepareReq的响应；MaxAcceptedProposal是自己曾经接受过的PN最大的Proposal，见第4.2节Accept(b)阶段；若曾经未接受过任何Proposal，则MaxAcceptedProposal为None；

Prepare阶段的作用是什么？Raft中并没有类似的阶段(其实，最终会发现，Prepare就是Raft的选主阶段)。这会涉及到Basic-Paxos中的最难点，第6节通过一些例子总结其作用；第11.2节也能看出其重要性。

Accept阶段 (4.2)

• Accept(a)：若Proposer收到majority数量个PrepareResp{Promise{n, Proposal}}，就pick一个Value，设为v，并向所有Acceptor发送Accept请求。Accept请求包含完整的Proposal(PN和Value)，记作AcceptReq{Proposal{n, v}}。怎么pick Value呢？查看已经收到的这majority个PrepareResp{Promise{n, Proposal}}:

  • 若其中的Proposal都为None，Proposer就可以随意pick一个Value作为v。这里的”随意”是指不受算法约束，一般v来自于客户端的请求；
  • 若其中的Proposal存在不为None的，就使用PN最大的那个Proposal的Value作为v；

• Accept(b)：一个Acceptor收到AcceptReq{Proposal{n, v}}时，若n>=MaxRespondedPN(即满足4.1节中的承诺2)就接受(accept)它。接受是指持久化MaxAcceptedProposal=Proposal{n, v}，并向Learner发送Proposal{n, v}。其中MaxAcceptedProposal表示自己曾经接受过的PN最大的Proposal；第4.1节的Prepare(b)中，Acceptor在PrepareResp中附带的就是它。

这就是Paxos决策的两个阶段了，强调两点：

• Acceptor只需要持久化两条信息：MaxRespondedPN和MaxAcceptedProposal；
• 为了清晰，把Acceptor对PrepareReq的处理叫做响应（respond），对AcceptReq的处理叫做接受（accept），下文将一直遵守这个约定；

熟悉Raft的同学可能会有疑问：Acceptor怎么没有向Proposer返回接受应答？Proposer也没有在接收到majority个应答之后选定Value？实现上可能确实这么做(比如ceph-monitor的Paxos实现)，但模型上，这是学习阶段的事，见第4.3节。

Learn阶段 (4.3)

在Accept(b)阶段，Acceptor在接受(accept)一个AcceptReq{Proposal{n, v}}的时候，会把Proposal发给Learner；Learner在接收到majority个Proposal{n, v}的时候，就学习到：Proposal{n, v}被选定(chosen)了，也称作v被选定了。

Proposal(及其Value)虽然是由Acceptor选定的，但是，是由Learner发现它被选定的，这个发现的过程就是学习。因为每个Acceptor完全基于自己记录的信息去决策要不要响应一个PrepareReq，要不要接受一个AcceptReq，不会也不可能考虑别的Acceptor，所以每个Acceptor并不知道最哪个Proposal被选定。当然，Proposer也不知道。这是分布式系统的本质，也是Learner在模型中如此重要的原因。最初我把Learner理解为被选定的Value的消费者或使用者，如复制状态机或者更上层的Client，这是不对的，Learner的作用是发现被选定的Proposal(及其Value)，所以它叫Learner而不是User或Consumer之类。

注意：

• Learner可能先收到Proposal{m, u}但没有达到majority个，后来又收到majority个Proposal{n, v}，这是完全正常的情况。按照算法的定义，后者被选定。
• 一个Basic-Paxos实例中，可能有多个Proposal被选定，但它们的Value一定是相同的，见第6节的例4。

假如系统中有M个Acceptor和N个Learner，按照Accept(b)阶段的描述，最多的时候会产生M*N个消息。基于非拜占庭这一假设，可以减少消息的个数：即指定一个或几个Learner，Acceptor只把接受的Proposal发给它们，由它们学习到哪个Proposal被选定，而其它Learner都向它们学习。为了形象，我们把这一个或几个特殊的Learner叫做中转Learner。

还有一个问题，假如majority个Acceptor都接受了一个Proposal，但所有的中转Learner都死了；等它们恢复的时候，就学习不到那个被选定的Proposal。一个直观的想法是，让Learner去轮询Acceptor，若能收到majority个相同的Proposal就知道它被选定了。但这是行不通的：因为轮询的时候可能又有Acceptor死了，Learner收不到majority个相同的Proposal。可行的办法是，Learner请求Proposer重新提议；根据算法的保证，在新的一轮中选定的一定是相同的Value，所以Learner在新一轮能学习成功即可。第6节的例4和这个场景类似。

角色映射 (5)

前面说到，熟悉Raft的同学可能会有疑问：Acceptor应该向Proposer返回接受应答，Proposer接收到majority个应答之后就选定Value。本节以ceph-monitor的Paxos为例，解释它们其实是一致的。

问题的根本在于角色映射。在ceph-monitor的Paxos实现里：

• Leader不只扮演Proposer，还扮演Learner的角色，并且是那个中转Learner(它其实还扮演Acceptor的角色，这里先不提)。
• Peon(可以认为是Raft里Follower)同时扮演Acceptor和Learner的角色，但都是非中转Learner。

所以，ceph-monitor的Paxos中，后半段消息流向就是这样的：

• Peon把对AcceptReq的接受应答发给Leader，其实是发给Learner(中转Learner)，因为Leader扮演了这一角色；
• Leader收到majority个应答之后就知道它提议的Proposal被选定了，进而开始commit操作，即Leader扮演的Learner学习到Proposal被选定；
• Commit操作: 持久化被选定的Value，回应client，并把Value告诉Peon，其实是把学习结果中转给其他Learner；

是不是和Raft非常一致？

举例 (6)

在推导（见第11节）之前，先通过一些例子直观感受一下Basic Paxos的运行过程，并尝总结其背后逻辑：虽然Prepare和Accept两个阶段看上去也不复杂，但是”唯一性”是怎么保证的？Prepare阶段的作用是什么？这些问题却不直观。

假设有：

• 3个Proposer: P1到P3；它们各自有一个唯一ID，叫做ServerId，分别为1，2，3；
• 5个Acceptor: A1到A5；
• 2个Learner: L1和L2；

并假设PN的格式:

• PN: {Round}.{ServerId}
• PN的比较方式：Round为主；ServerId为辅；

下面的例子从假单到复杂，一方面展示Basic-Paxos是如何运行的；另一方面，尽量多的展示典型的异常情况是如何被处理的。另外，着重体现Prepare阶段的作用，因为Prepare阶段是最难理解的。

• 例1：基本流程

  1. P1生成PN=100.1，并向Acceptor发送PrepareReq{100.1}；
  2. A1,A2,A3收到PrepareReq{100.1}；它们之前没有响应过任何PrepareReq也没接受过任何Proposal，所以都响应P1：持久化MaxRespondedPN=100.1，并返回PrepareResp{Promise{100.1, None}}；
  3. P1收到A1,A2,A3的响应，已达majority，并且返回的Proposal全是None，故自主pick值V，并向Acceptor发送AcceptReq{Proposal{100.1, V}}；
  4. A1,A2,A3收到AcceptReq{Proposal{100.1, V}}，都接受：持久化MaxAcceptedProposal=Proposal{100.1, V}，并把Proposal{100.1, V}发给L1；
  5. L1收到3个Proposal{100.1, V}，已达majority，故学习到：V被选定；

• 例2：Prepare的第一个作用

  1. P1生成PN=100.1，并向Acceptor发送PrepareReq{100.1}；

  2. A1,A2,A3收到PrepareReq{100.1}，都响应P1：持久化MaxRespondedPN=100.1，并返回PrepareResp{Promise{100.1, None}}；

  3. P1收到A1,A2,A3的响应，已达majority，自主pick值V，并向Acceptor发送AcceptReq{Proposal{100.1, V}}；

  4. 由于网络延迟，只有A3收到AcceptReq{Proposal{100.1, V}}，接受：持久化MaxAcceptedProposal=Proposal{100.1, V}，并把Proposal{100.1, V}发给L1；

  5. L1只收到1个Proposal{100.1, V}，没有学习到选定值；

  6. P2生成PN=101.2，并向Acceptor发送PrepareReq{101.2}；

  7. A1,A4,A5收到PrepareReq{101.2}，都响应P2：持久化MaxRespondedPN=101.2，并返回PrepareResp{Promise{101.2, None}}。注意：A1响应P2是因为它的MaxRespondedPN=100.1小于101.2，返回None是因为第d步没有收到P1的AcceptReq{Proposal{100.1, V}}，故自己的MaxAcceptedProposal为None；

  8. P2收到A1,A4,A5的响应，已达majority，因为都为None所以自主pick值U，并向Acceptor发送AcceptReq{Proposal{101.2, U}}；

  9. A1,A4,A5收到AcceptReq{Proposal{101.2, U}}，接受并把Proposal{101.2, U}发给L1；

  10. L1收到3个Proposal{101.2, U}，学习到：U被选定；

  11. P1在第c步发出的AcceptReq{Proposal{100.1, V}}，由于网络延迟，现在被A1,A2,A4,A5收到。但A1,A4,A5的MaxRespondedPN=101.2（见第g步）大于100.1，故不接受。A2接受：持久化MaxAcceptedProposal=Proposal{100.1, V}，并把Proposal{100.1, V}发给L1；

  12. L1在第e步收到1个Proposal{100.1, V}，现在又收到1个，共2个，还是没有达到majority；故V没有被选定；

注意：通过第k步可以看出Prepare的第一个作用：屏蔽过时请求（PrepareReq和AcceptReq）（本例中是被网络延迟的AcceptReq{Proposal{100.1, V}}）。试想，若没有这个屏蔽，A1,A4,A5中再有一个接受它，加上A3和A2，就达到majority，V就又被选定了；之前U已被选定（第j步），违背”唯一性”要求了。将来我们知道：屏蔽过时请求其实就是Raft中Follower拒绝过时的Leader发来的消息。

另外：到现在，A2和A3的MaxAcceptedProposal还是Proposal{100.1, V}。这完全没有关系，因为从模型上讲，单个Acceptor接受的Proposal是什么根本不重要，它们一起才重要。即便是A1,A4或A5，虽然它们的MaxAcceptedProposal是Proposal{101.2, U}，但它们各自也不知道U被选定这一事实。

• 例3：接受多个Proposal

  1. P1生成PN=100.1，并向Acceptor发送PrepareReq{100.1}；

  2. A1,A2,A3收到PrepareReq{100.1}，都响应P1：持久化MaxRespondedPN=100.1，并返回PrepareResp{Promise{100.1, None}}；

  3. P1收到A1,A2,A3的响应，已达majority，自主pick值V，并向Acceptor发送AcceptReq{Proposal{100.1, V}}；

  4. 由于网络原因，只有A3收到AcceptReq{Proposal{100.1, V}}，接受：持久化MaxAcceptedProposal=Proposal{100.1, V}，并把Proposal{100.1, V}发给L1；

  5. L1只收到1个Proposal{100.1, V}，没有学习到选定值；

  6. P2生成PN=101.2，并向Acceptor发送PrepareReq{101.2}；

  7. A3,A4,A5收到PrepareReq{101.2}；A4,A5响应P2并返回PrepareResp{Promise{101.2, None}}；A3响应P2并返回PrepareResp{Promise{101.2, Proposal{100.1, V}}}，因为之前A3的MaxRespondedPN=100.1小于101.2且MaxAcceptedProposal=Proposal{100.1, V}；

  8. P2收到A3,A4,A5的响应，已达majority，响应中Proposal{100.1, V}的PN最大（只有它一个，所以最大），故pick其值V，并向Acceptor发送AcceptReq{Proposal{101.2, V}}；

  9. A3,A4,A5收到AcceptReq{Proposal{101.2, V}}，接受并把Proposal{101.2, V}发给L1；

  10. L1收到3个Proposal{101.2, V}，学习到：V被选定；

注意：P3接受过2个Proposal。在第2.10节的推导过程中，将会看到接受多个Proposal是必要的。

另外，第h步中，P2 pick值V是一个偶然情况：假设第g步响应P2的不是A3,A4,A5而是A1,A4,A5（和例2一样），那么在第g步P2得到的全是None就会自主pick值。因为之前没有值被选定，所以无论P2 pick什么值都是正确的：本例pick的V，或者这里的假设发生时自主pick值，都是正确的。在下面例4中我们将看到，第r步的时候P2一定要pick值W才是正确的，因为W已经被选定了。

• 例4：Prepare的第二个作用

  1. P1生成PN=100.1，并向Acceptor发送PrepareReq{100.1}；

  2. A1,A2,A3收到PrepareReq{100.1}，都响应P1：持久化MaxRespondedPN=100.1，并返回PrepareResp{Promise{100.1, None}}；

  3. P1收到A1,A2,A3的响应，已达majority，自主pick值V，并向Acceptor发送AcceptReq{Proposal{100.1, V}}；

  4. 由于网络原因，只有A3收到AcceptReq{Proposal{100.1, V}}，接受：持久化MaxAcceptedProposal=Proposal{100.1, V}，并把Proposal{100.1, V}发给L1；

  5. L1只收到1个Proposal{100.1, V}，没有学习到选定值；

  6. P2生成PN=101.2，并向Acceptor发送PrepareReq{101.2}；

  7. A1,A2,A4收到PrepareReq{101.2}；都响应P2并返回PrepareResp{Promise{101.2, None}}；注意：A1和A2的MaxRespondedPN=100.1小于101.2且MaxAcceptedProposal=None；

  8. P2收到A1,A2,A4的响应，已达majority，自主pick值U，并向Acceptor发送AcceptReq{Proposal{101.2, U}}；

  9. A2收到AcceptReq{Proposal{101.2, U}}，接受并把Proposal{101.2, U}发给L1；

  10. 现在，L1共收到1个Proposal{100.1, V}和1个Proposal{101.2, U}，没有学习到选定值；

  11. P3生成PN=102.3，并向Acceptor发送PrepareReq{102.3}；

  12. A1,A4,A5收到PrepareReq{102.3}；都响应P3并返回PrepareResp{Promise{102.3, None}}；注意：A1和A4之前的MaxRespondedPN=101.2小于102.3且MaxAcceptedProposal=None；

  13. P3收到A1,A4,A5的响应，已达majority，自主pick值W，并向Acceptor发送AcceptReq{Proposal{102.3, W}}；

  14. A1,A4,A5收到AcceptReq{Proposal{102.3, W}}，接受：持久化MaxAcceptedProposal=Proposal{102.3, W}，并把Proposal{102.3, W}发送给L1；

  15. L1学习到：W被选定；

  16. P2又生成PN=103.2，并向Acceptor发送PrepareReq{103.2};

  17. A1,A2,A3收到PrepareReq{103.2}；A1返回PrepareResp{Promise{103.2, Proposal{102.3, W}}}；A2返回PrepareResp{Promise{103.2, Proposal{101.2, U}}}；A3返回PrepareResp{Promise{103.2, Proposal{100.1, V}}}；

  18. P2收到A1,A2,A3的响应，已达majority。由于其中A1返回的Proposal{102.3, W}的PN=102.3最大（大于100.1和101.2），故pick值W，并向Acceptor发送AcceptReq{Proposal{103.2, W}}；

  19. A1,A2,A3收到AcceptReq{Proposal{103.2, W}}，接受并把Proposal{103.2, W}发送给L2；

  20. L2学习到：W被选定；

注意：通过第r步可以看出Prepare的第二个作用：发现已被选定的值。这一点非常重要，因为从在第p步P2生成了一个更大的PN，在一切正常的情况下它pick的值将会被选定。但问题是，之前W已经被选定了。所以，算法必须保证P2在第r步中会pick W。如何保证呢？就是通过Prepare阶段询问majority个Acceptor，各自接受过什么Proposal，然后找出PN最大的那个，其值就一定是W。其原因留待第11.2节解释。

Progress (7)

Basic-Paxos可能出现活锁的情况：

时间	Proposer P1	Proposer P1
t1	生成PN=100.1；发出PrepareReq并获得majority个响应；
t2		生成PN=101.2；发出PrepareReq并获得majority个响应；
t3	发出AcceptReq{Proposal{100.1}}，但被majority拒绝，因为100.1<101.2；
t4	生成PN=102.1；发出PrepareReq并获得majority个响应；
t5		发出AcceptReq{Proposal{101.2}}，但被majority拒绝，因为101.2<102.1；
t6		生成PN=103.2；发出PrepareReq并获得majority个响应；
t7	发出AcceptReq{Proposal{102.1}}，但被majority拒绝，因为102.1<103.2；
t8	生成PN=104.1；发出PrepareReq并获得majority个响应；
t9		发出AcceptReq{Proposal{103.2}}，但被majority拒绝，因为103.2<104.1；
t10		生成PN=105.2；发出PrepareReq并获得majority个响应；
…	…	…

为了解决这个问题，论文[1]提出”选Leader”的方案，即选出一个特定的Proposer，请求只由它发起。John Ousterhout和Diego Ongaro在Paxos summary[2]中给出了一个选举方案：

• 每个server有一个不同的ID；
• 每隔T毫秒，每个server发一个heartbeat给所有其他server；
• 一个server将自动变成Leader，如果满足：最近2T毫秒内没有收到ID更大的server发来的heartbeat；

仔细想就会发现，这个方案是不严格的，有时可能选出多个Leader，例如：

• 3个server，ID分别是1，2和3
• 3发给2的heartbeat发送丢包；
• 2T毫秒之后，2和3都变成Leader；

但Basic-Paxos的正确性是不依赖于这个选举算法的：即使出现了上面选出2个Leader的情形，也只是增大了活锁的概率，没有破坏正确性。所以选举算法在大多数情况下能工作就可以了。

另外，在第8节中将看到，把这个过程叫做选Leader并不合适，这里暂且这么叫。

思考 (8)

在Basic-Paxos流程中，Accept和Learn阶段非常容易理解：就是一个Proposal若被多数派接受，就选定了。我们试图加深对Prepare理解。用白话说Prepare就是这样的：

“我现在想发起第n轮投票；大伙儿请把n之前接受的PN最大的Proposal告诉我。虽然你们各自都不知道是否存在一个Proposal被选定（被你们多数派接受），更不知道自己接受的PN最大的那个Proposal是否被选定，坦白的说，我也不知道，但是，我有办法保证：只要存在被选定的Proposal，我提议的Value一定和它的Value一样，这样大家才能完成任务（保证唯一性）嘛。之前你们要是没有选定一个Proposal的话（可能都没有接受过Proposal，也可能各自接受过但没有形成多数派），那这个Value就由我定。同时你们要向我保证：不再参与比n小的提议。你们可以参与更大的，这没问题：因为假如我现在提议的Value被选定，更大的提议也一定会和我的Value一样”。

至于这个”办法”还是上面说的：从PrepareResp找PN最大的那个，第11.2节将解释这个办法为什么可行。

本质上Prepare就是选举：

• 得到majority的PrepareResp{Promise}不就是得到多数派的选票吗？
• Acceptor承诺不接收小于（等于）n的PrepareReq/AcceptReq，不就是拒绝过时的Leader吗？
• PN不就是term吗？当然，从这个角度上理解，叫做PN（Proposal Number）看上去不太合适。但在Basic-Paxos中，提议每个Propsal都选举新Leader（都进行一次Prepare），一任Leader一个Proposal，所以Leader的term也就等价于Propsal Number了。

当然，除了选举之外Prepare还有一个作用，就是发现之前选定的值。在那个叫Paxos的希腊小岛上实行的是民主制度，如果前任Leader提议的法案已经被多数派接受但还没推行的话，那么新任Leader有义务推行它，所以新任Leader在他的选举誓言中说：你们接受过什么法案，请告诉我，我有办法找出已经被多数派接受的法案，然后重新提议这个法案。若是不存在被多数派接受的法案，那么我作为Leader可以提出新的法案。

如第7节所述，为了满足Progress需求，论文[1]中提出选Leader的方案（论文第2.4节和2.5节），由这个Leader来进行Basic-Paxos流程。整个流程变成：

• Leader选举；
• Prepare阶段；
• Accept阶段；

这让人费解：Prepare本质上就是选举Leader，前面怎么还有一个Leader选举呢？其实活锁问题本质上是，P1选举成功之后（Prepare成功）提议之前（Accept阶段之前），P2夺取了领导权（P2 Prepare成功）导致P1无法提议；然后P1在P2提议之前再夺取领导权，如此反复。所以，论文[1]中所说的Leader选举形象点说其实是提名一名候选人，只有这名候选人能够发起选举（然后提议Proposal）。后来在论文[4]中找到了印证，它把Basic-Paxos流程描述成这样：

很明显，其中Prepare阶段被Coordinator选举取代（Coordinator就是Leader），并且论文[4]后面描述的Coordinator选举过程就是Prepare阶段。

明确了Prepare的本质就是选举，就很容易想到，每次提一个Proposal都选举一次是明显的浪费。Multi-Paxos的一个优化就在于此，这是后话。

细节与优化 (9)

论文[1]上说：Proposer把PrepareReq发给一个majority集合，等收到它们的PrepareResp的时候，再把AcceptReq{Proposal}发给同一majority集合。这里有两个细节：

• 细节1: PrepareReq和AcceptReq是发给一个majority集合的，而不是发给所有Acceptor的；
• 细节2: PrepareReq和AcceptReq是发给同一个majority集合的（当然处理这两个消息的也是同一majority集合），而没说能不能是不同majority集合；

其实这不是必须的。考虑Prepare的两个作用:

• 发现已被选定的值：无论从哪些Acceptor回复了PrepareResp，只要数量达到majority，Proposer都能够发现已被选定的值（若有），即pick PN最大的。见第11.2节。
• 屏蔽过时请求：PrepareReq和AcceptReq由两个不同的majority集合处理，并不破坏屏蔽作用，看下面的例子。

Proposer P1把PrepareReq{120.1}发给所有Acceptor，但只收到了A1,A2,A3的响应（持久化MaxRespondedPN=120.1并返回PrepareResp）。而A4和A5有两种可能：

• a) MaxRespondedPN=119.3，可以响应，但请求(PrepareReq{120.1})或者响应(PrepareResp)被丢包。
• b) MaxRespondedPN=121.2，收到了PrepareReq{120.1}，但由于承诺1不能响应。这是可能发生的，比如之前P2生成PN=121.2并发起PrepareReq{121.2}，但只有A4,A5收到并响应了，其它Propoer和Acceptor根本不知道PN=121.2存在过。

P1收到A1,A2,A3的PrepareResp已达majority, 就把AcceptReq{Proposal{120.1, v}}又发给所有Acceptor，但由于丢包A1,A2没收到，只有A3,A4,A5（一个不同于A1,A2,A3的集合）收到了。A3接受，而对于A4和A5，分别看上面的两种情况：

• a) MaxRespondedPN=119.3，小于120.1，满足承诺2，所以接受它。但需要同时更新MaxRespondedPN=120.1。这一点在论文[1]上没有提，因为它假设两次请求是发给同一个majority集合的，MaxRespondedPN在响应PrepareReq的时候已经更新了。
• b) MaxRespondedPN=121.2，大于120.1，违背承诺2，所以丢弃它，导致没有选定Proposal（如果A1,A2没有丢包，本该选定的）。然而，没有选定总不会破坏唯一性；假如经过很长的延迟，A1,A2又收到AcceptReq并接受了，还能选定。

所以，针对这两个细节，有两个优化：

• 优化1：PrepareReq和AcceptReq都发给所有Acceptor；
• 优化2：Acceptor在接受AcceptReq的时候，不但要更新MaxAcceptedProposal还要更新MaxRespondedPN；

下面我们引用John Ousterhout和Diego Ongaro在Implementing Replicated Logs with Paxos[2]中的描述，这两个人就是Raft的作者，也是大神级的人物。他们就考虑了这两个细节并做了优化。

为了看明白他们的描述，需要统一一下变量名：

• minProposal就是我们的MaxRespondedPN；为什么他们叫min而我们叫max呢？这是着眼点不同导致的：min是说将来能响应的最小的PN，max是说过去响应的最大的PN，本质上是相同的。
• acceptedProposal和acceptedValue合起来就是我们的MaxAcceptedProposal。

可见Acceptors的第6步acceptedProposal=minProposal=n就是优化2。另外，显然PrepareReq和AcceptReq也都是发给所有Acceptor的，即优化1。

• 细节3：论文[1]说必须保证不同Proposal的PN是不同的，不同Proposer可以从不交集合中获取PN（我们使用的”{Round}.{ServerId}”就是一种不交集合）。从正确性上，这就够了，不要求后生成的PN比之前的大：试想majority的Acceptor的MaxRespondedPN都在100.x以上了，Proposer P3崩溃重启之后从Round=1开始使用PN=1.3去提议，一定得不到majority的响应，然后它自增Round再提议，再失败，再自增，如此反复，最终能够生成有效的PN。这虽然是正确的，但效率比较低。

论文[1]中有两处和这个相关的优化：

“It is probably a good idea to abandon a proposal if some proposer has begun trying to issue a higher-numbered one. Therefore, if an acceptor ignores a prepare or accept request because it has already received a prepare request with a higher number, then it should probably inform the proposer, who should then abandon its proposal. This is a performance optimization that does not affect correctness.”

“Each proposer remembers (in stable storage) the highest-numbered proposal it has tried to issue, and begins phase 1 with a higher proposal number than any it has already used.”

结合起来就是，就是：

• 优化3：Proposer可以从Acceptor对PrepareReq或AcceptReq的拒绝中获取最新的PN，这样就不用反复递增；其次，Proposer持久化自己见过的最大的PN，这样崩溃重启也不会丢失。

John Ousterhout和Diego Ongaro在Accept阶段采用了优化3（上面图中Proposers的第6步，遇见更大的PN就回到第1步重新生成PN）不过在Prepare阶段（即第4步）没有采用。相反，ceph-monitor的Paxos里，在Prepare阶段（handle_last函数）采用了这个优化，但在Accept阶段没有采用，原因可能是在Accept阶段，即使个别Acceptor返回更大PN，但还是有希望得到majority的接受的。

John Ousterhout和Diego Ongaro在Paxos Summary[3]中也描述了Proposer如何更新并持久化maxRound：

• 细节4：Prepare阶段，n和MaxRespondedPN的比较，到底是大于还是大于等于？论文[1]强调使用大于；John Ousterhout和Diego Ongaro在Implementing Replicated Logs with Paxos[2]中使用的是大于，但在Paxos Summary[3]中使用的是大于等于。

通过细节3可知，两个Proposer不可能使用相同的PN，所以大于和大于等于都可以：不同Proposer发来的PrepareReq的PN肯定是不同的；若Acceptor收到两个PN相同的PrepareReq，它们一定来自于同一Proposer，是同一PrepareReq多次重传，多次响应它也是正确的。

• 优化4：Prepare阶段，n和MaxRespondedPN的比较关系使用大于等于。这样，两个阶段的比较就一致了，比较好记。不过从效率上讲，重复持久化一次没有必要。好在这种情况在实现上不会发生，因为高层协议比如RPC能够处理网络重传。

重新描述 (10)

基于第9节对一些细节的讨论和优化，我们重新描述完整的Basic-Paxos流程。首先：

• 把Propser和中转Learner合到一个实体里，即Propser/Learner合体，这样更接近于实现；
• Acceptor对AcceptReq的回复消息记作AcceptResp，返回给Propser/Learner合体；其中包含Rejection{n}或Proposal{n, v}二选一；前者是发给Proposer角色的，以便其执行优化3；后者是发给Learner角色的，以便其学习选定值；
• 对PrepareResp也进行一下扩展，包含Promise{n, Proposal}或Rejection{n}二选一；

算法的开始于Proposer从Client接收到inputValue：

Prepare(a): Proposer

• maxRound++；
• 生成PN：n=maxRound.ServerId；
• 持久化maxRound；
• 向所有Acceptor发送PrepareReq{n}；

Prepare(b): Acceptor

• 接收PrepareReq{n}；
• 若n>=MaxRespondedPN（优化4）：持久化MaxRespondedPN=n；回复PrepareResp{Promise{n, MaxAcceptedProposal{k, w}}}；
• 若n<MaxRespondedPN：回复PrepareResp{Rejection{MaxRespondedPN}}；

Accept(a): Proposer

初始化：pickedPN=0; pickedValue=inputValue; count=0;

• Proposer接收PrepareResp{Promise{n, Proposal{k, w}}}或者PrepareResp{Rejection{m}}；
• 若接收到的是PrepareResp{Rejection{m}}且m>n（m<n为过时消息；m=n不可能）：maxRound = m.Round；放弃本轮；回到Prepare(a)重新开始。优化3。
• 若接收到的是PrepareResp{Promise{n, Proposal{k, w}}}：count++；若k>pickedPN，则pickedPN=k且pickedValue=w（即pick PN最大的Proposal的Value）；
• 若count>=majority：向所有Acceptor发送AcceptReq{Proposal{n, pickedValue}}；

Accept(b)：Acceptor

• 接收AcceptReq{Proposal{n, v}}；
• 若n>=MaxRespondedPN：持久化MaxAcceptedProposal=Proposal{n, v}和MaxRespondedPN=n（优化2）；向Proposer/Learner发送AcceptResp{Proposal{n, v}}；
• 若n<MaxRespondedPN：向Proposer/Learner发送AcceptResp{Rejection{MaxRespondedPN}}；

Learn: Proposer/Learner

初始化：count=0; maxRejectionPN=0;

• 接收AcceptResp{Proposal{n, v}}或者AcceptResp{Rejection{m}}；
• 若接收到的是AcceptResp{Rejection{m}}且m>n（m<n为过时消息；m=n不可能）：若m>maxRejectionPN则maxRejectionPN=m；
• 若接收到的是AcceptResp{Proposal{n, v}}：count++；
• 若count>=majority：学习到选定值v；
• 若到达超时count依然小于majority且maxRejectionPN>n（有Acceptor返回拒绝消息）：maxRound = maxRejectionPN.Round；放弃本轮；回到Prepare(a)重新开始。优化3。

综上，在Basic-Paxos中要持久化的信息是：

Proposer：maxRound；
Acceptor: MaxRespondedPN和MaxAcceptedProposal；

推导 (11)

前面描述了Basic-Paxos的流程，并使用例子的方式详细解释它是如何运行的，本节介绍推导过程。推导方式和论文[1]类似：从问题出发，提出一个草案，发现草案中的矛盾点，修正草案，如此反复直到问题解决。但这里尽量使过程容易理解，特别是放弃论文中的”在归纳证明中提出方法”的方式（这一点很不好理解，通常是先提出方法然后再证明方法有效），而采用一种不严谨但很符合直觉的方式，见第11.2节。

问题已于第2节提出，下面直接针对问题提出草案并进行修正。

过程 (11.1)

草案1 - Single Acceptor

• 只有一个Acceptor；
• Proposer把提议的值发给Acceptor；
• Acceptor选定第一个接收到的值；

显然”唯一性”能够被满足。但在假设的”非拜占庭模型”中，服务器可能随时宕机，一旦唯一的Acceptor发生故障，整个服务就不可用。

草案2 - Multi Acceptor：接受第一个值

• 有一组（多个）Acceptor；
• Proposer把提议的值发给多个Acceptor；
• Acceptor可以接受提议的值；
• 如果一个值被majority个Acceptor接受，那么它就被选定；因为任何两个majority必然存在非空的交集，所以能够保证”唯一性”。
• Acceptor必须接受它收到的第一个值，因为这样才能满足：只有一个Proposer提议的时候，也能选定值（Progress需求）；

但这导致一个问题：假如多个Proposer同时提议多个不同的值，每个Acceptor都接受它收到的第一个，那么可能形成不了多数派，极端情况是每个Acceptor都接受了一个不同的值，也就无法选定一个值了，不满足Progress需求。

草案3 - Multi Acceptor：接受每一个值

为了解决草案2中的问题，就要求一个Acceptor必须能够接受多个值。假如Acceptor接受它收到的每一个值，显然行不通：Proposer P1提议的值v1得到了majority个Acceptor的接受（即v1被选定）；然后P2提议了值v2（v2不等于v1），又得到majority个Acceptor接受（v2被选定），就违反”唯一性了”。所以Acceptor既要接受多个值又不能接受每一个值，必须有一定的策略来决定哪些可以接受，哪些不能接受。

草案4 - 引入Proposal

为了解决草案3中的问题，引入Proposal的概念：Proposal包含一个Proposal Number(PN)和Value(就是我们关注的变量的值)，PN=n且Value=v的Proposal记作Proposal{n, v}。

• 有一组（多个）Acceptor；
• Proposer把它提议的Proposal发给多个Acceptor；
• Acceptor可以接受Proposal;
• 如果一个Proposal被majority个Acceptor接受，那么Proposal（及其Value）就被选定；
• Acceptor可以接受多个Proposal;
• 进而，允许一到多个Proposal被选定，但是在多个Proposal被选定的情况下，必须保证它们的Value是相同的，这样才能保证”唯一性”。

注意和草案3的区别：Proposer不直接提议一个Value，而是提议一个Proposal（其中包含值）。既然Acceptor只接受第一个或接受每一个都不行，草案4基于Proposal制定一个策略：Acceptor可以接受多个Proposal（当然也会根据策略拒绝一些Proposal），进而可能出现多个Proposal被选定的情况，但要求：如果Proposal{m,u}和Proposal{n,v}都被选定，必须要保证u和v相等（其中m不等于n）。 见第6节的例4：第n步和第s步分别选定了Proposal{102.3,W}和Proposal{103.2,W}。

如何保证呢？首先把Proposal按PN从小到大排序，如果能做到：

• R1：若Proposal{n,v}被选定了，以后选定的Proposal（满足PN>n）的Value一定是v；

就足够了。因为只有被Acceptor接受的Proposal才能被选定，所以，只要能做到：

• R2：若Proposal{n,v}被选定了，以后Acceptor接受的Proposal（满足PN>n）的Value一定是v；

就足够了。又因为只有被Proposer提议的Proposal才能被Acceptor接受，所以，只要能做到：

• R3：若Proposal{n,v}被选定了，以后Proposer提议的Proposal（满足PN>n）的Value一定是v；

就足够了。

到目前为止，推理都是显而易见的，问题最终归结于如何做到R3。在解决这问题之前（下一节），我们体会一下引入Proposal（特别是其中的PN）的意义：Proposal的引入，使我们能够对Proposer发出的提议进行排序。假如没有顺序，由于网络延迟、重传等原因，导致各个角色接收消息的顺序和消息被发出的顺序不同，例如Acceptor1先接收到v1后接收到v2，而Acceptor2先接收到v2后接收到v1；Acceptor3接收到一个十分钟之前提议的v3如何处理，如此等等，使问题异常复杂。不是说不排序就一定无解，但Basic-Paxos的解是基于顺序的：可以看见，前面的推导逻辑是基于顺序一步步把问题归结于R3的。到目前，问题已经相当清晰了：只要能够满足R3，草案4就是可行的。

证明 (11.2)

如何满足R3呢，方法就是引入Prepare阶段，Proposer在收到majority个PrepareResp之后，需要pick一个Value进行提议：

• 若PrepareResp中附带的Proposal都为None，Proposer就可以随意pick一个Value作为v；
• 若PrepareResp中附带的Proposal存在不为None的，就使用PN最大的那个Proposal的Value作为v；

这就能满足R3：若在此之前Proposal{n,v}已经被选定（被多个Acceptor接受）了，这里Proposer pick的Value一定是v。下面证明它:

• 假设Proposal{n,v}是第一个被选定的Proposal（即任何PN<n的Proposal都没有被majority接受），那么在Proposal{n,v}被选定的那一刻，我们按MaxAcceptedProposal.PN从小到大对Acceptor排序，结果一定形如图a、b或c，而绝不可能形如图d（注：图中圆柱的高低代表MaxAcceptedProposal.PN的大小；{n,v}表示Acceptor的MaxAcceptedProposal=Proposal{n,v}；绿色部分表示MaxAcceptedProposal.Value=v）：因为图d的产生说明之前一定存在Proposer发出过AcceptReq{Proposal{o,w}}，其中o>n；进而说明PrepareReq{o}一定得到了majority个Acceptor的响应；进而说明一定存在majority个Acceptor，其MaxRespondedPN为o；由于o>n，Proposal{n,v}不可能再被majority个Acceptor接受，即不可能被选中。矛盾。另外注意，在图a、图b和图c中，A1和A3的MaxRespondedPN还是有可能大于n的：试想，一个Proposer发了一个PN比较大的PrepareReq，而A1和A3响应了它，但没达到majority。这既不会导致图d出现，也不妨碍Proposal{n,v}被选定。

• 以图c为基础考虑第n+1轮（图a和图b等价于图c）:

  • Prepare阶段：假设获得了majority个PrepareResp，无论这个majority集合如何构成，里面PN最大的Proposal一定是Proposal{n,v}，所以pick的值一定为v。直观的看，即使从最左开始取majority=3个，也一定能够至少包含一个绿色的（绿色的在右边，故PN最大）。

  • Accept阶段：发出AcceptReq{Proposal{n+1,v}}；由于：因素a. 丢包，和因素b. A1和A3的MaxRespondedPN可能大于n+1，可能出现下面几种情况：

    • 图c1：A4,A2,A5没收到AcceptReq{Proposal{n+1,v}}；A1和A3或没收到或拒绝（MaxRespondedPN>n+1）；最终Proposal没有被选定；
    • 图c2：A4,A2,A5没收到AcceptReq{Proposal{n+1,v}}；A3或没收到或拒绝；A1收到并接受； 最终Proposal没有被选定；
    • 图c3：A4和A5没收到AcceptReq{Proposal{n+1,v}}；A1和A3或没收到或拒绝；A2收到并接受；最终Proposal没有被选定；
    • 图c4：A4,A2和A5收到AcceptReq{Proposal{n+1,v}}并接受；Proposal被选定，但值还是v；
    • 图c5：A1,A3和A5收到AcceptReq{Proposal{n+1,v}}并接受；Proposal被选定，但值还是v；
    • 图c6：所有Acceptor收到AcceptReq{Proposal{n+1,v}}并接受；Proposal被选定，但值还是v；

• 继续以图c1-c6为基础考虑第n+2轮。其实还有更多的组合，但它们和图c1-c6都有一个共同特点：绿色部分越来越多，即MaxAcceptedProposal.Value=v的Acceptor越来越多。以它们为基础进行第n+2轮的Prepare阶段，只要能够获得majority个PrepareResp，其中PN最大的Proposal的Value一定是v：图c都能满足这一点，图c1-c6更能满足，因为绿色部分变多了。直观的看，即使从最左开始取majority=3个，也一定能够至少包含一个绿色的（绿色的在右边，故PN最大）。

• 依次归纳：n+3，n+4，……，绿色的部分只可能保持不变或越来越多，所以只要Prepare阶段成功得到majority个PrepareResp，其中PN最大的Proposal的Value一定是v；进而提议Proposal的Value一定是v。

这就证明了：一旦Proposal{n,v}被选定，以后的Proposer只可能pick到值v。

小结 (12)

抛开形式化证明，Basic-Paxos本来还是比较易懂的，但是Lamport大神从证明推导出方法的论述方式不容易理解，大家还是习惯于先给出方法，然后证明这个方法是正确的。然而这已经是”Paxos Made Simple”了。不管怎样，至此Basic-Paxos已经比较清楚了，并且已经可以看出Raft的雏形：

• Prepare阶段对应Raft的Leader election；
• Raft一次选举，多次Propose；而Basic-Paxos一次选举(Prepare)，只Propose一次；
• Raft选举的时候能够保证所选出的Leader一定拥有所有committed logs，所以不需要从Follower拉取Log；而Basic-Paxos不能保证这一点（只要能生成足够大的PN就能够当选为Leader），所以选举（Prepare）的时候，需要把committed value搜集过来（即PrepareResp里附带的MaxAcceptedProposal）；

参考文献 (13)

1. Paxos Made Simple
2. Paxos summary
3. Implementing Replicated Logs with Paxos
4. Paxos Made Live - An Engineering Perspective
5. In Search of an Understandable Consensus Algorithm